[Work Log] Work Log

January 11, 2015

Finished training.

training_result = 

         final_const_variance: 1.1669e-04
  final_branch_const_variance: 1.7636e+03
        final_linear_variance: 1.4425e+03
      final_geodesic_variance: 195.4912
         final_geodesic_scale: 0.0065
                  final_noise: 0.0776

training_result.initial

ans =

         const_variance: 831.7886
  branch_const_variance: 0.8552
        linear_variance: 0.1183
     euclidean_variance: 1.7367
        euclidean_scale: 1.0000
      geodesic_variance: 225.8247
         geodesic_scale: 1.0000
      epipolar_variance: 1.7367

These just don't make sense. It allows for almost zero total translation, but lots of pert-curve translation (const_variance vs. branch_const_variance). Linear variance allows for way too much scaling. Geodesic variance seems sensible, but the (inverse-squared) geodesic scale is way too low... Basically this becomes a stand-in for const_variance. Perhaps this is just a local minimum, we could try fixing const_variance to some large number and forcing geodesic variance to serve its intended purpose.

But the strangest thing is that

I sampled some curves from this prior, and they are about what I'd expect: rotated and scaled with very little nonrigid deformation. Below is a sample, along with the mean tree barely visible in the center:

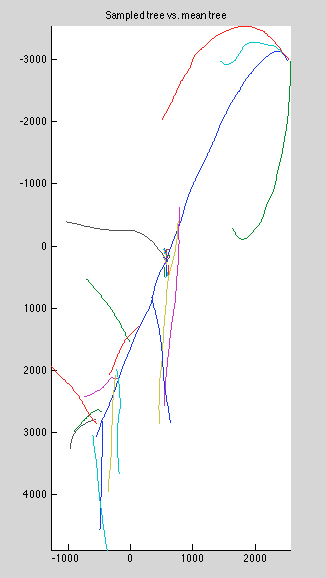
tree sample

Ruled-out causes of error:

Training observations

The simulated annealing algorithm is very sensitive to our local minima. It can sometimes find a good result in less than 500 iterations, but other times it gets stuck after less than 100 and never improves. I can probably tweak the annealing schedule to increase temperature earlier(is "reannealing" the right value to tweak?").

The patternsearch algorithm beats simulated annealing after only 16 iterations (vs. 5k or more). Annealing really struggles to get out of that minimum.

Surprisingly, after adding a seventh parameter (for branch-specific affine deformation), patternsearch totally fails to find a good minimum starting from default parameters. Initializing it with the result of the six-parameter model gives much better results. This suggests a coarse-to-fine strategy for training might work well in general. However, this is a very specific case: the six-parameter model was flexible enough to explain the data quite well, but was overly permissive -- it allowed too many nonsensical solutions. Adding the seventh parameter introduced an alternative explanation of the data, one requiring less nonrigid deformation.

To try: genetic algorithm; particle swarm; simplex method; start pattern search from SA result; globalsearch; grid search with multistart

Globalsearch & multistart w/ simplex fminunc

Misc results

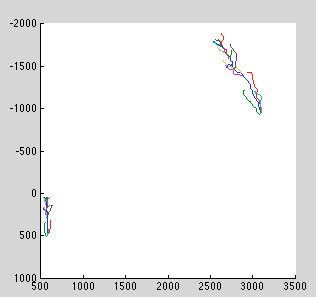
log-likleihood = -3.1787e+03
training_result = 

         final_const_variance: 6.0197e+06
  final_branch_const_variance: 1.5774e-09
        final_linear_variance: 1.6250
      final_geodesic_variance: 238.6891
         final_geodesic_scale: 0.0039
         final_noise_variance: 0.1487

Not bad. Lots of geodesic variance to account for distortion. Why is const variance so high? Linear variance seems a bit high, but reasonable.

It might be a good idea to allow each branch to have a linear distortion relative to its initial point.

log-likelihood = -2.5318e+03
training_result = 

       final_const_variance: 2.3156e+09
final_branch_const_variance: 2.4988
      final_linear_variance: 33.8221
    final_geodesic_variance: 1.7165e+03
       final_geodesic_scale: 0.0029
       final_noise_variance: 0.0880

Much smaller noise variance, much higher for all other variances. const variance is astronomical... is the optimizer exploiting numerical error arising from a poorly-conditioned matrix?

log-likelihood = -2.4848e+03
training_result =

       final_const_variance: 0.1383
final_branch_const_variance: 1.7466
      final_linear_variance: 5.4218e-04
    final_geodesic_variance: 378.6715
       final_geodesic_scale: 0.0048
       final_noise_variance: 0.0832

This is close to what I would hope for -- small constant and linear variance, most variance coming from deformation. Still, the scale is fairly short (~14 pixels), allowing for quite a bit of deformation.

Ran for several thousand more iterations. Seem to be converging.

log-likelihood = -2.4799e+03
training_result =

       const_variance: 0.0717
branch_const_variance: 3.2826
      linear_variance: 0.0028
    geodesic_variance: 401.4291
       geodesic_scale: 0.0047
       noise_variance: 0.0831

Running from scratch with the "pattern_search" algorithm, I got excellent results very quickly:

log-likelihood = -2.4256e+03
training_result =

         const_variance: 261.7339
branch_const_variance: 3.0796
      linear_variance: 0.0035
    geodesic_variance: 165.2169
       geodesic_scale: 0.0063
       noise_variance: 0.0821

These are the most sensible results yet! Moderately large constant variance , small but nonnegligible branch constant variance. A touch of linear variance to rotations. Smaller deformation variance in response to larger const variance. Yes!

Adding a new parameter assigning independent affine deformation variance to each branch. This should allow less variance to be allotted to geodesic_variance, which should improve marginal-likelihood.

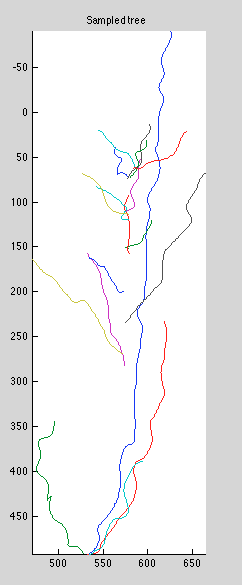
Initial training pass failed to find the old local minimum. Restarting it using the previous optimum resulted in very nice parameters:

log-likelihood = -2.3107e+03
training_result = 

        const_variance: 291.9853
 branch_const_variance: 2.0196
       linear_variance: 0.0366
branch_linear_variance: 0.0516
     geodesic_variance: 12.7402
        geodesic_scale: 0.0136
        noise_variance: 0.0796

Note the dramatic drop in geodesic variance and increase in marginal likelihood. On the other hand, the (corrected) geodesic scale dropped from(~12 to ~8), meaning slightly higher effective dimension. The resulting tree looks much closer to the original shape than previous models.

Previous model had a problem: allowing each curve to affine-transform independently results in parents drifting away from children, which in reality isn't possible. We need each child to inherit the covariance of the parent, which we accomplish by simply taking the dot-product of the "geodesic" index.

The pattern_search algorithm is having a hard time finding a better set of

Starting from the same position as previous starting point, results in a worse log-likelihood:

log-likelihood = -2.3131e+03
training_result = 

        const_variance: 3.1017e-25
 branch_const_variance: 2.9157
       linear_variance: 0.0326
branch_linear_variance: 0.0575
     geodesic_variance: 12.5426
        geodesic_scale: 0.0137
        noise_variance: 0.0796

Zero const variance is troubling. Other parameters are mostly unchanged, except slightly higher branch_const_variance. It seems the translation component was mostly used to align curves affected by parallax.

Actually, zero const variance isn't so surprising, because our now model alls branches to pivot around their starting point, and the root of the tree hardly moves between views. What movement there is could be solved by pivoting the whole tree around it's center, using the global affine transformation.

It seems we have a redundant representation here. The branch affine transformations subsume the global affine transformation, unless there's evidence that a multi-level type of model is reasonable (which it might be).

Starting from the result of the previous run gives slightly better results, but still not better than the "bad" model used previously.

log-likelihood = -2.3122e+03
training_result = 

        const_variance: 498.3842
 branch_const_variance: 2.9623
       linear_variance: 0.0400
branch_linear_variance: 0.0523
     geodesic_variance: 12.0562
        geodesic_scale: 0.0138
        noise_variance: 0.0799

Now optimization approach, adding one dimension at a time and reoptimizing. Results are almost identical to second-to-last run:

log-likelihood:  -2.3131e+03
training_result = 

        noise_variance: 0.0800
     geodesic_variance: 12.3965
        geodesic_scale: 0.0136
branch_linear_variance: 0.0576
 branch_const_variance: 2.9157
       linear_variance: 0.0327
        const_variance: 8.3205e-09

Again, low const_variance, but we manually can do 1D optimization to improve it:

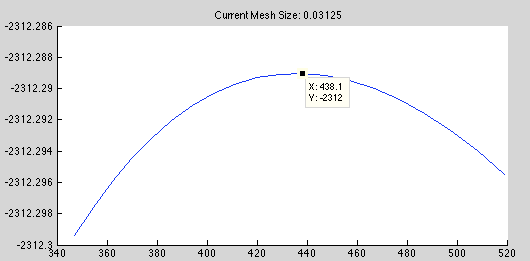
training_result = 

        noise_variance: 0.0800
     geodesic_variance: 12.3965
        geodesic_scale: 0.0136
branch_linear_variance: 0.0576
 branch_const_variance: 2.9157
       linear_variance: 0.0327
        const_variance: 435.8995

Some plots showed that at low const_variance, the terrain become rocky, making search difficult.

Forcing noise variance to be 1.0 results in much smoother priors:

training_result = 

        noise_variance: 1
     geodesic_variance: 15.9174
        geodesic_scale: 0.0019
branch_linear_variance: 0.0485
 branch_const_variance: 3.7438
       linear_variance: 0.0348
        const_variance: 685.7670

This kind of makes sense, since our point-correspondence algorithm has mean error of 0.5, even if correspondences are perfect. In many cases, correspondences aren't perfect, because the triangulation metric used to find correspondences isn't sufficiently informative to infer the true correspondence. So forcing i.i.d. noise variance to some minimum value prevents the prior from taking up that noise.

misc notes

Try different deformation model - cubic spline?

euclidean affine transform

next:

Dangling tasks:

Posted by Kyle Simek
blog comments powered by Disqus