[Work Log] Debugging ML gradient
Implemented end-to-end ML gradient in curve_ml_derivative.m. Now testing.
Fixed some obvious math errors, changes reflected in writeup. Now getting close results, but still getting some noticible error, see below.
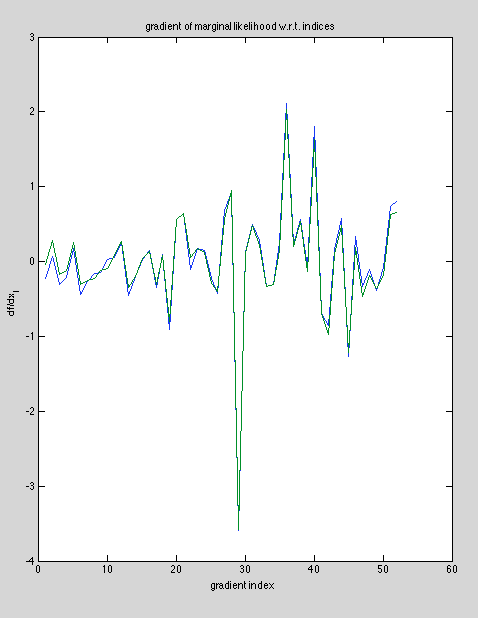
(Green is reference, blue is testing).
Results are qualitatively close, but enough error to suggest a bug
Debugging so far:
- two different impementations for analytical gradient
- two different implementations for numerical gradient
- one-sided and two-sided numerical gradient.
- several delta sizes for numerical gradient {0.0001, 0.0001, ..., 0.1, 1.0}
- Using emperical Δ' (from finite differences) for analytical gradient.
- using both cholesky and direct method for matrix inversion (testing for numerical issues).
- sanity check: used intermediate values from gradient computation to compute function output.
To try:
- use numerical gradient for K' instead of from Δ′.
Is it possible we're not handling XYZ independence properly?
Noticed that using a really large delta (~1.0) actually improves resuls. Is it possible we're seeing precision errors being exacerbated somewhere in the end-to-end formula?
Strategy: pick gradient element with mode error and run the following test. For each derivative component (dK, dU, dV, dg), compare against reference to determine where the error is being introduced.
Index #22
dK/dt has 1e-4 error in on-diagonal. Off diagonals max out at 1e-10.
delta: 0.01 on-diagonal error ~ 1e-3 below-and-right < 1e-4
delta: 0.001 on-diagonal error ~ 1e-4 other error < 1e-10
delta: 0.0001 on-diagonal error ~ 1e-5 below and right ~ 1e-6
delta: 0.00001 on-diagonal error ~ 1e-6 below and right ~ 1e-4
Decreasing delta improves on-diagonal, makes below-and-right worse.
This is weird that we're even getting error in dK/dt, because it passed our unit test. Well, Δ′ passed our unit test, but that's basically the same thing...
However, reduced error at delta of 1e-3 seems to agree with our end-to-end test. So maybe this is the culprit.
It's also surprising that there's so much fluctuation as delta changes. The computation for K isn't that involved, and we shouldn't be hitting the precision limit yet. However, the values do get pretty large, so maybe that's a factor.
Magnitude of the original matrix does seem to be a factor. Look at this slice of the error matrix (dK_test - dK_ref):
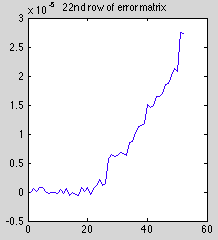
Compare that to the diagonal of the matrix we did finite differences on. This is basically a plot of the cubed index values.
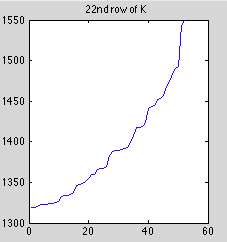
The error seems to increases in lockstep with the magnitude of the original values (note the jumps occur at similar positions). I guess this is to be expected, but I was surprised at the magnitude.
I'm still curious why the error starts to climb exactly at index #22, i.e. the index we're differentiating with respect to.
This plot should drive home the relationship between index valuea end error.
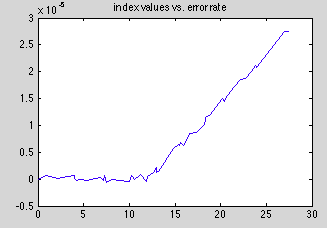
Definitely a linear relationship after index #22.
A back of the envelope error analysis suggests that below index 22, the analytical derivative's approximation error is not a function of X, but above index 22, it's a linear function of X. This is a pretty reasonable explanation, although I couldn't get the exact numbers to explain the slope of the line ( the slope seems high). But at this hour I wouldn't trust my error analysis as far as I could throw it, quantitatively speaking.
We can attempt to place an upper bound on the error estimate by propagating the error in K' through the differential formula for g'. Assume every nonzero element of K has error of 3e-5 (the maximum we observed emperically). Let this error matrix be ϵ, and it has the same banded structure as K′. Then we can replace K′ with ϵ in the formula for g′ (formula (1) in the writeup) to get the upper bound error on our data-set.
>> 0.5 * z' * Epsilon * z
ans =
-1.1758e-05
We can conclude that the error we're observing is coming from somewhere else.
To conclude for tonight, we're seeing some error in dK/ds, but probably nothing out of the ordinary, and it has low enough error that we can hopefully ignore it.
Lets look a the outher sources of error tomorrow, i.e. U' and V'
Posted by Kyle Simek